There are various formulae in aviation which suggest that, for small changes and to a first order approximation, each 1% drop in weight should improve the IAS by 1% or 2% (I don't remember the formula).
Yet I see no such change for my TB20, which persistently does 138kt IAS (low level e.g. 3000ft) at 11.3usg/hr, 2400rpm, regardless of loading which could be anywhere between MTOW-20% and MTOW.
I see less than 1kt of variation, which can be due to anything.
What could be the explanation?
I don't have data like you do but I have observed significant speed differences depending on weight distribution in my TR182. The more I push the envelope to the back of the airplane, the faster it flies. In cruise, I can slide back both front row seats and see a 2-3kt speed increase.
I have since then bought a folding water tank which I put in the back of my airplane when the rear seats are not filled. The explanation is quite simple I think -- the elevator produces a down force which "eats" from your propulsion energy and the heavier the tail is, the less force required. The airliners pump fuel from/to the elevator to optimize weight distribution.
Some gliders have water tanks in the tail to get maximum efficiency by optimum C of G positioning. It takes some careful calculation to get it right, obviously getting it wrong could have consequences!
The more I push the envelope to the back of the airplane, the faster it flies
I think that has to be the answer (reduced elevator drag when more heavily loaded, because the extra weight inevitably ends up in the back) but when I have posted on this topic elsewhere, nobody offered this explanation.
I call this a good result 
which persistently does 138kt IAS (low level e.g. 3000ft) at 11.3usg/hr, 2400rpm
Off-topic: I can't see these numbers with my TB20. Can you (maybe in separate thread) list your performance, settings and consumption data for range of altitudes (e.g. from 2000ft to FL140)? Thanks in advance.
Emir
I have seen the previous discussions, (I even participated  ),
but in them you said that the weight difference was due to different fuel loads,
and that the fuel tanks are exactly on the aircraft CG.
),
but in them you said that the weight difference was due to different fuel loads,
and that the fuel tanks are exactly on the aircraft CG.
I did have one idea since the last time round: could the fuel weight change the wing camber, (depressing the lower surface)? This could increase the wing's pitching moment, and then you get the familiar chain of more anti-torque down-force required at the tail, so more lift required at the wing, so more drag at both, and so worse mpg.
I have absolutely no idea if the effect would be significant, nor which way round it is! To get the effect you describe, the pitching moment would have to increase with decreasing fuel load, which is possible, I suppose.
Interesting puzzle though...
Never the less, for any increase in AUW the wing has to produce greater lift, hence greater drag. As lift is (I think) proportional to drag it seems like 1% more weight should require 1% more power for the same speed. Is this, on VP a/c, disguised by a tiny more the throttle setting or hard to discern fuel flowincrease ?
Optimising C of G rearwards within the permitted envelope is an established ploy to reduce drag.
As is setting correctly (if the design allows it) the tail plane to wing A of A to something on average like -1 Degree. This can also reduce drag from the elevator in cruise being deployed noticeably out of alignment to the tailplane to compensate for unecessary up or down forces. In home or kit built a/c it's not an unknown fact.
mike hallam.
There are various formulae in aviation which suggest that, for small changes and to a first order approximation, each 1% drop in weight should improve the IAS by 1% or 2% (I don't remember the formula).
If you don't remember the formula, why are you surprised when the formula you've guessed doesn't work?!
The power required by an aircraft is proportional to (v^^3 + W^^2/v) where v is the dimensionless speed relative to minimum drag (at max weight) and W is the weight relative to max.
W 0.800 0.850 0.900 0.950 1.000
v
0.800 1.312 1.415 1.525 1.640 1.762
0.850 1.367 1.464 1.567 1.676 1.791
0.900 1.440 1.532 1.629 1.732 1.840
0.950 1.531 1.618 1.710 1.807 1.910
1.000 1.640 1.723 1.810 1.903 2.000
1.050 1.767 1.846 1.929 2.017 2.110
1.100 1.913 1.988 2.067 2.151 2.240
1.150 2.077 2.149 2.225 2.306 2.390
1.200 2.261 2.330 2.403 2.480 2.561
1.250 2.465 2.531 2.601 2.675 2.753
1.300 2.689 2.753 2.820 2.891 2.966
1.350 2.934 2.996 3.060 3.129 3.201
1.400 3.201 3.260 3.323 3.389 3.458
1.450 3.490 3.547 3.607 3.671 3.738
1.500 3.802 3.857 3.915 3.977 4.042
1.550 4.137 4.190 4.246 4.306 4.369
1.600 4.496 4.548 4.602 4.660 4.721
1.650 4.880 4.930 4.983 5.039 5.098
1.660 4.960 5.010 5.062 5.118 5.177
1.670 5.041 5.090 5.142 5.198 5.256
1.680 5.123 5.172 5.224 5.279 5.337
1.690 5.206 5.254 5.306 5.361 5.419
1.700 5.289 5.338 5.389 5.444 5.501
If your operating point is 1.0 (minimum drag speed) a 5% reduction in weight is roughly equivalent to a 5% increase in speed -- i.e. the power required for W = 0.95 and v = 1.05 is about the same as the power required for W = 1.00 and v = 1.00.
If your operating point is 1.7, you need to reduce W to about 0.93 to make up for an increase in v from 1.69 to 1.70. In other words a 5% reduction in weight is roughly equivalent to a 0.5% increase in speed.
So if your TB20 minimum drag speed is 90 kt, and you cruise at 150 kt, you're going to see that latter sort of ratio. By contrast, most jets at altitude cruise not far from minimum drag speed, which is why they care about every extra gallon of extra fuel they have to carry, while you and I just fill the tanks.
Put another way, very little of your drag at cruise speed is the weight-dependent induced drag. It's almost all weight-independent parasite drag.
I think bookworm has it right.
Another way to see it is to look at the Lift and Drag curves plotted against angle of attack. At low angles of attack, (i.e. high speeds), the Lift coefficient is nicely linear, but the Drag coefficient is almost flat.
If we ignore induced drag, then theoretically an increase in weight has no effect on Drag: the Lift/Drag ratio simply adjusts accordingly. Paradoxically the L/D ratio improves with weight!
A better way to check out the Lift/Drag ratio is to look at Drag Polars, i.e. CL plotted aginst CD. The slope from the origin to a point gives the L/D ratio. The slope at any point gives the incremental L/D ratio.
This is a (randomly chosen) example on Wikipedia:
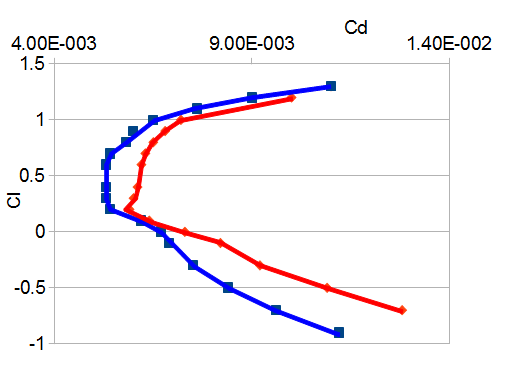
from this page: Drag Polar
Taking the blue line as an example, we see there is a cruising CL region 0.2-0.7 where CD does not change, and significantly different weights could be carried for no extra Drag cost.
I doubt the real world is so simple, and I know nothing about TB20s, but suddenly Peter's results do look plausible!
Thanks, both of you! That explains it.
I fly at 140kt IAS, but Vbg is about 95kt.